DFA = NFA
우선, DFA가 만들 수 있는 언어는 모두 NFA로도 만들 수 있다. 이는 정의에 의해 자명하다. 그렇다면 여기서 당연히 NFA가 만들 수 있는 언어는 모두 DFA로도 만들 수 있는지에 대한 궁금증이 생긴다. 결론부터 말하면 맞다. 이를 증명하기 전에, 앞서 보았던 NFA 하나를 DFA로 바꿔보자.

위 NFA를 $M$이라고 하면 $M=(\{q_0, q_1, q_2\}, \{0, 1\}, \Delta, q_0, \{q_2\})$이다. $\Delta$의 함숫값을 구하면
- $\Delta^*(q_0, 0) = \{q_0\}$
- $\Delta^*(q_0, 1) = E(\Delta(q_0, 1)) = \{q_0, q_1, q_2\}$
- $\Delta^*(q_1, 0) = \Delta^*(q_1, 1) = \{q_2\}$
이다. 이제 우리는 상태 집합이 $\mathcal{P}(\{q_0, q_1, q_2\})$의 부분집합인 DFA를 만들어 볼 것이다. 당연히 초기 상태는 $\{q_0\}$일 것이다. 그 DFA의 전이 함수를 $\delta$라고 하면
- $\delta(\{q_0\}, 0) = \Delta^*(q_0, 0) = \{q_0\}$
- $\delta(\{q_0\}, 1) = \Delta^*(q_0, 1) = \{q_0, q_1, q_2\}$
로 정의하는 것이 자연스럽다. 이제 $\{q_0, q_1, q_2\}$라는 상태가 생겼으니 이 상태의 전이 또한 정의해야 한다. 마찬가지로
- $\delta(\{q_0, q_1, q_2\}, 0) = \Delta^*(q_0, 0)\cup\Delta^*(q_1, 0)\cup\Delta^*(q_2, 0) = \{q_0, q_2\}$
- $\delta(\{q_0, q_1, q_2\}, 1) = \Delta^*(q_0, 1)\cup\Delta^*(q_1, 1)\cup\Delta^*(q_2, 1) = \{q_0, q_1, q_2\}$
로 정의하는 것이 자연스럽다. 이렇게 연쇄적으로 상태와 그 전이를 정의하면 아래와 같은 DFA가 만들어진다 (편의상 상태의 $q$는 생략하고 첨자만으로 표시하였다).
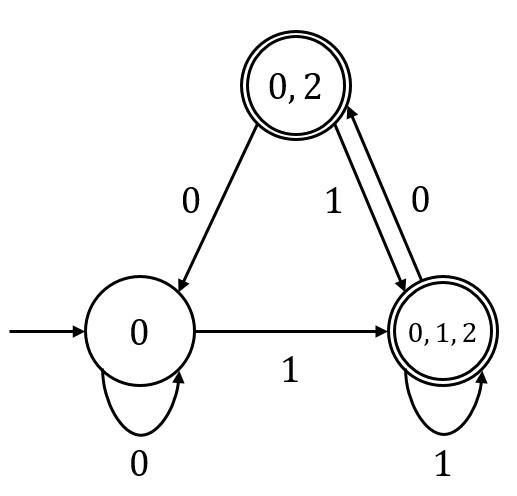
최종 상태는 NFA의 최종 상태인 $\{q_2\}$를 포함하고 있는 모든 상태로 정했다. 몇 가지 예시를 넣어보면 원래 NFA와 같은 역할을 한다는 것을 알 수 있다. 일반적인 경우도 이 예시와 비슷하다. NFA $N = (Q, \Sigma, \Delta, q_0, F)$가 주어졌을 때 DFA $D = (\mathcal{P}(Q), \Sigma, \delta, E(q_0), \{X\in \mathcal{P}(Q) : X \cap F\neq\phi\})$를 만들 수 있다. 엄밀한 증명은 생략하겠다 (귀납법으로 가능하다).
Why NFA?
NFA는 무언가 직관적인 것 같으면서도 비 직관적이다. 그렇게 느껴지는 이유는 실제로 우리가 살고 있는 자연에는 비결정 적인 요소들이 많아 다음 상태가 결정되지 않는 것이 직관적인데, 컴퓨터는 그렇지 않고 다음 상태가 결정되어 있기 때문에 컴퓨터에 대입해보면 비 직관적으로 느껴진다. 하지만 DFA로 바꾸게 되면 NFA의 비결정성은 제거가 가능하다. 따라서 NFA를 이용해 비결정적인 문제 상황을 직관적으로 표현한 후에 DFA로 바꾸는 과정을 거치면 훨씬 효율적으로 작업할 수 있다. 즉, NFA는 현실(비결정적인 세상)과 컴퓨터(결정적인 세상)를 이어주는 중요한 interface 같은 역할을 한다.
* 이 글은 서울대학교 박근수 교수님의 '오토마타이론' 강의자료에 기반을 두고 있고, 교수님의 허락을 받고 포스팅을 진행함을 밝힌다.
'CSE > Automata Theory' 카테고리의 다른 글
| [Automata Theory] Nondeterministic Finite Automata (0) | 2022.09.19 |
|---|---|
| [Automata Theory] Deterministic Finite Automata (0) | 2022.09.16 |
| [Automata Theory] Regular Expression (0) | 2022.09.14 |
| [Automata Theory] Language (0) | 2022.09.14 |
| [Automata Theory] Introduction (0) | 2022.09.14 |

